Bad proofs
1. Proof by questionable mathematics
Theorem 1.1: All positive integers are equal.
Proof:
It suffices to show that for any two positive integers, A and B, A = B. Further, it suffices to show that for all N > 0, if A and B are positive integers which satisfy MAX(A, B) = N then A = B.
We proceed by induction. If N = 1, then A and B, being positive integers, must both be 1. So A = B.
Assume that the theorem is true for some value k. Take A and B with MAX(A, B) = k+1. Then MAX((A-1), (B-1)) = k. And hence (A-1) = (B-1). Consequently, A = B.
Hence, A = B for all positive integers A and B by induction. Q.E.D.
Theorem 1.2: All positive integers an interesting property.
Proof:
Assume the contrary. Let A be the lowest non-interesting positive integer. But, hey, that's a pretty interesting property about A. Hence, we have a contradiction. Q.E.D.
Here is a slightly more rigorous version of Theorem 1.2.
Theorem 1.3: Every natural number can be unambiguously described in 14 words or less.
Proof:
Suppose there is some natural number which cannot be unambiguously described in fourteen words or less. Then there must be a smallest such number. Let's call it n.
But now n is "the smallest natural number that cannot be unambiguously described in fourteen words or less." This is a complete and unambiguous description of n in fourteen words, contradicting the fact that n was supposed not to have such a description!
Therefore, all natural numbers can be unambiguously described in fourteen words or less. Q.E.D.
Theorem 1.4: The integral of cosine over its first period is zero.
Proof:
Q.E.D.
Theorem 1.5: Zero equals unity, i.e. 0 = 1.
Proof:
Q.E.D.
The following generalizes Theorem 1.5.
Theorem 1.6: Any integer equals its successor, i.e. n = n+1 any integer n.
Proof:
Q.E.D.
Theorem 1.7: A dollar is equal to one penny.
Proof:
We shall use the conventional physics notation and write units behind the numbers. That is, 1 $ means 1 dollar, and 5 c means five cents. Proceeding:
1 $ = 100 c = (10 c)2 = (0.1 $)2 = 0.01 $ = 1 c. Q.E.D.
2. Proof by Semantic Silliness
Theorem 2.1: A cat has nine tails.
Proof:
No cat has eight tails. A cat has one tail more than no cat. Therefore, a cat has nine tails. Q.E.D.
Theoremm 2.2: A sheet of paper is a lazy dog.
Proof:
A sheet of paper is an ink-lined plane.
An inclined plane is a slope up.
A slow pup is a lazy dog.
By transitivity, a sheet of paper is a lazy dog. Q.E.D.
Theorem 2.3: A penut-butter and jelly sandwhich is better than life itself.
Proof:
A peanut-butter and jelly sandwhich is better than nothing.
Nothing is better than life itself.
By transitivity, a peanut-butter and jelly sandwhich is better than life itself. Q.E.D.
Proof by Cliche
Theorem 3.1 (The Salary Theorem): The less you know, the more money you make.
Proof:
It is known in universities that knowledge is power, hence

Similarly, it is known in business that time is money, whence

From physics, we have by definition that power is the ratio of work to time, so that

Making the substitutions above, we have

Solving for money, we get:

Thus, as knowledge approaches zero, money approaches infinity, regardless of the amount of work done. Q.E.D.
Theorem 3.2: Girls are evil.
Proof:
It is known throughout all cultures athat girls require both time and money, hence

Similarly, it is known in business that time is money, whence

Substitution yields

From the Bible, we know that money is the root of all evil, whence

Substituting again yields
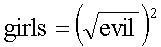
Squaring on the right-hand side of the equation yields

establishing the result. Q.E.D.
In fact, there is a flaw in this argument, which was subsequently corrected.